ロボットの設計や制御では、ロボットの各関節部を原点にもつ複数の座標系を扱います。
そして、ある座標系での物体の位置が、基準とする座標系から見た時にどのように表されるかを必要に応じて計算する必要があります。
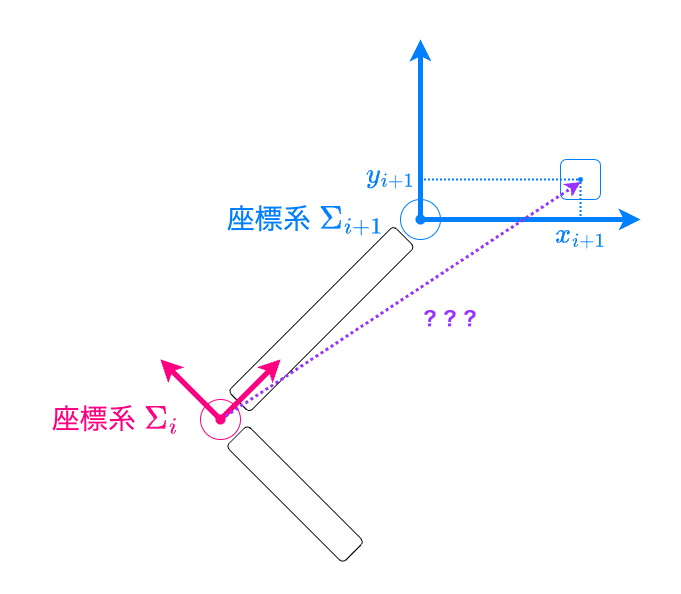
座標系Σiから見た時の位置???を知りたい
例えば、ロボットアームを考えると、エンドエフェクタの位置を制御したい時、アームの手先の座標系における位置が入力となりますが、エンドエフェクタの位置を事前に計画したい時、地面に固定されたグローバルな座標系から見た位置を知る必要があるからです。
ある座標系での位置を他の座標系での表現に変換するために必要となるのが、同次変換行列です。
本記事では、2次元座標を題材に、同次変換行列の基礎を高校レベルから丁寧に解説します。また、記事要約とPythonコードを統合したJupyter Notebookを付属していますので、ぜひハンズオン形式でやってみてください。
実用上の、多関節ロボットにおける3次元上での座標変換は、大変複雑になることがありますが、本記事の内容が理解できていれば、容易く理解できるかと思います。

途中で、用語や数式が分かんなくなったらどうすればいいのかな。

Pythonで手を動かして分かれば十分だぜ。
付属のJupyter Notebookは、高校数学の授業の教材としてもご使用頂ける内容です。一次変換の意味を視覚的に見ることのできる例として、ご利用ください。
一般的に、図形の変形や座標の変換に用いられる、回転・拡大、並進(並行移動)、シアー(剪断)の4種類の変換を総称して、アフィン変換といいます。
同次変換行列は、(正確には)アフィン変換と、アフィン変換を組み合わせた変換を簡潔に記述するための形式です。
本記事では、アフィン変換の詳細には踏み込みません。その代わり、代表的なアフィン変換のうち、ロボティクス分野での使用頻度の高い回転・拡大・並進について丁寧に解説します。
高校数学の教科書に登場する回転・拡大を復習します。
まず、横に\(a\)倍、縦に\(b\)ズーム(拡大)するような行列は、 \(\begin{bmatrix}a & 0 \\ 0 & b \\ \end{bmatrix}\)で表されました。
次に、角度\(\theta\)だけ回転させるような行列は、\(\begin{bmatrix} cos\theta & -sin\theta \\ sin\theta & cos\theta \\ \end{bmatrix} \)と表されました。
2次元の座標1点\((x, y)\)に対する変換を見てみます。例えば点(10, 10)を\(x\)方向に2.0倍、\(y\)方向に0.5倍ズームすると、
\( \begin{bmatrix} 2.0 & 0 \\ 0 & 0.5 \\ \end{bmatrix} \begin{bmatrix} 10 \\ 10 \\ \end{bmatrix} = \begin{bmatrix} 20 \\ 5 \\ \end{bmatrix} \)
となり、点(10, 10)が点(20, 5)に移動するのでこれで良いですね。
複数の点を一度に変換する場合、N点の座標、つまり、
\( (x_i, y_i)^T,\ i = 1, 2, …, N \)
を並べたN x 2の行列に変換行列をかければ良いです。再び、ズームを例に確認すると、
\( \begin{bmatrix} a & 0 \\ 0 & b \\ \end{bmatrix} \begin{bmatrix} x_1 & \cdots & x_N \\ y_1 & \cdots & y_N \\ \end{bmatrix} = \begin{bmatrix} ax_1 & \cdots & ax_N \\ by_1 & \cdots & by_N \\ \end{bmatrix} \)
となります。各点の\( x \)座標が\( a \)倍、\(y\)座標が\(b\)倍になっていますのでこれでいいですね。
Pythonプログラムで確認してみましょう。Pythonでは、変換する座標と変換行列はnumpy配列で管理し、行列式はnumpy.matmul()で計算します。
ここでは、長方形にズーム(拡大縮小)変換を施し、変換の前後の図形をmatplotlibで描画して確認します。
コード全文は、Jupyter Notebookの1.1節をご覧ください。ポイントだけ説明します。
まず、ズームの変換行列を作成します。
長方形は4点で決まります。変換前の長方形を、4点の点群としてnumpy配列で定義します。
ズーム変換を施します。変換行列と図形は、共にnumpy配列で表現できているので、単に行列同士の掛け算(行列式の計算)で変換が可能です。
ズーム前後の長方形をmatplotlibで図示します。

変換行列\(\begin{bmatrix} a & 0 \\ 0 & b \end{bmatrix} \)は、座標の原点中心のズームであることに注意してください。
座標の原点中心のズームであるということは、図形上の各点を表すベクトルの\(x\)成分の大きさが\(a\)倍、\(y\)成分の大きさが\(b\)倍される操作であるということです。
次に、円に回転・拡大の変換を行ってみましょう。まず、ズームの変換行列と、回転の変換行列を作ります。
同時に、変換する円の半径と中心の座標をそれぞれ定数RADIUS, CENTERで定めています。
半径が3.0, 中心が(2.0, 2.0)の円を作成します。ここでは、角度をパラメータとして、360点の点群として円を表現しました。
circleは、\( \begin{bmatrix} x_1 & \cdots & x_N \\ y_1 & \cdots & y_N \\ \end{bmatrix} \)の行列になっていることに注意してください。
中心を原点とする半径\(r\)の円上の点の座標は\(P = ( rcos\theta, rsin\theta )\)であり、中心が原点とは限らない一般の円上の点の座標は、その中心を点\(O\)すると、\(\vec{O} + \vec{P}\)とベクトルで扱う方が計算しやすい。
円にズームと回転をそれぞれ適用してみます。一度、行列表現に落とし込めば、非常に簡潔に書けることがわかるかと思います。
変換前後の円をmatplotlibで図示します。
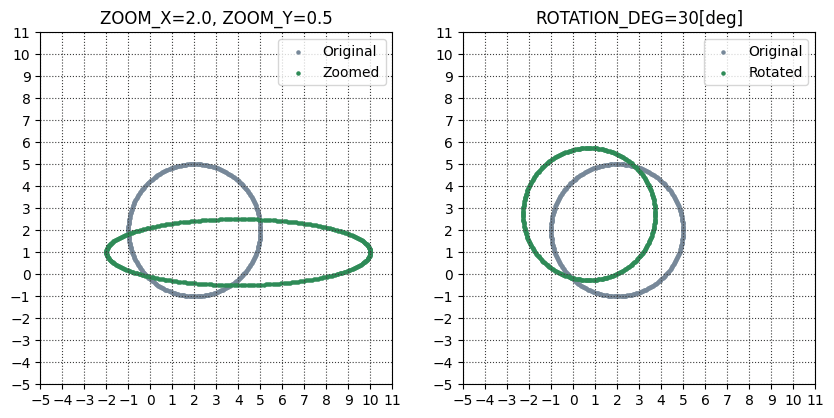
回転・拡大の次に、並進(並行移動)に対応する変換を考えます。
単純な発想としては、以下のように単純な加算で点を並進することができるでしょう。
\( \begin{bmatrix} x \\ y \end{bmatrix} + \begin{bmatrix} p \\ q \end{bmatrix} = \begin{bmatrix} x + p \\ y + q \end{bmatrix} \)
しかしながら、実用上このように並進を行うことはありません。回転拡大と同様に、行列積で変換できるような変換行列を使用します。
実は、2次元座標上の点を並進する変換は、あえて次元を1つ増やした、3×3の正方行列を使用する必要があります。
2次元座標上の位置\((x, y)\)を、\(x\)方向に\(p\), \(y\)方向に\(q\)だけ並進する変換行列は以下のようになります。
並進の変換行列:\( \begin{bmatrix} 1 & 0 & p \\ 0 & 1 & q \\ 0 & 0 & 1 \\ \end{bmatrix} \)
3×3の変換行列との積を取れるように、位置にもあえて不要な次元を1つ加えて、\((x, y)^T\)ではなく、\((x, y, 1)^T\)としておきます。
計算によって確認してみます。
\( \begin{bmatrix} 1 & 0 & p \\ 0 & 1 & q \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix} = \begin{bmatrix} x+p \\ y+p \\ 1 \\ \end{bmatrix} \)
計算結果の3列目だけは無視し、1列目、2列目を見ると、x -> x + p, y -> y + qと移動しており、正しく計算できていることがわかります。
これが、並進の変換行列です。
コード全文は、Jupyter Notebookの1-2節にあります。
回転・拡大と同様に変換行列を作り、点群として表現した円を変換します。並進の変換行列が3×3であることに注意してください。
変換前後の円を、matplotlibで図示します。\(x\)方向に1.0, \(y\)方向に3.0の並進が、図を見ても分かるかと思います。
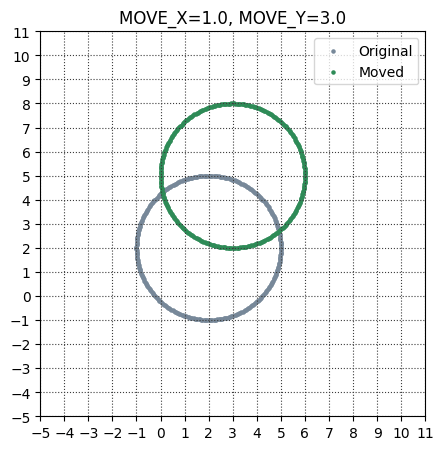
アフィン変換のうち、回転・拡大・並進の3種類の変換行列を確認し、matplotlibで図示することにより確認を行いました。
以下は、今までの内容のまとめと、今後使用する用語の説明です。
- アフィン変換とは一般的に、回転・拡大・並進の3種類に、剪断(シアー)(参考リンク)を加えた4種類の変換及び、それらを組み合わせた変換の総称である。
- 計算のためのダミー次元を1個付与した\( (x, y, 1)^T \)のような座標のことを同次座標という。
並進の変換行列のように、同次座標との行列積を取ることにより変換を行う変換行列のことを、同次変換行列といいます。
「回転と拡大」で説明した2×2の変換行列は、同次変換行列ではありません。
しかし、形状の異なる2×2の変換行列と3×3の変換行列では行列積をとることができないため不便です。本章では、回転・拡大変換を表す3×3の同次変換行列を定義し、それを実際に使ってみます。
先に、回転、拡大変換を同次変換行列で表したいモチベーションを説明します。
同次変換行列の計算だけ確認できれば良い方は、Jupyter Notebookの2-1節をご覧になるか、次まで飛ばしてください。
ロボティクスでは、\(\theta\) 回転してから、\(x, y\)方向にそれぞれ\(p, q\)だけ並進した後、\(x, y\)方向にそれぞれ\(a, b\)倍ズームする、といった複雑な変換は普通に出てきます。
仮に、回転変換を表す3×3の変換行列\(R(\theta)\), 拡大変換を表す3×3の変換行列\(Z(a, b)\)を作れるのであれば、上記の変換は以下のように表されます。
変換前の位置\(\boldsymbol P = \begin{bmatrix} x \\ y \end{bmatrix}, \)変換後の位置\(\boldsymbol P’ = \begin{bmatrix} x’ \\ y’ \end{bmatrix}\)とすると、
\( \boldsymbol P’ = \boldsymbol M\left(p, q\right) \boldsymbol Z\left(a, b\right) \boldsymbol R\left(\theta\right) \boldsymbol P\)
\( \boldsymbol T = \boldsymbol M\left(p, q\right) \boldsymbol Z\left(a, b\right) \boldsymbol R\left(\theta \right) \)とすると、\( \boldsymbol P’ = \boldsymbol T \boldsymbol P\)
変換を1つの行列式で表せることや、事前に変換\( \boldsymbol T \)を1つの行列として計算できることは、計算機を使用する上で大きなメリットとなります。
次の疑似コードのように、行列積の計算をGPUにより並列化できるからです。
「回転と拡大」で出てきた図形の点群としての表現\( \begin{bmatrix} x_1 & \cdots & x_N \\ y_1 & \cdots & y_N \\ \end{bmatrix} \)を思い出しましょう。

図形の点数が多くなったら、並列化しないと遅くなって困るワン。

一つ行列式で表せるようにしておいて、GPUを使うのがベストだね。
本節の話は、ロボティクス分野の話に限らず、データ分析の世界でも当てはまります。
例えば、主成分分析(Primary Component Analysis, PCA)で行う、高次元のデータの低次元への圧縮は、線形変換そのものであり、行列式により表されます(参考リンク)。
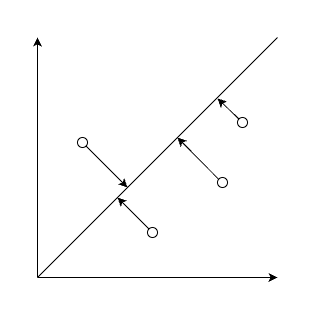
データ分析では変換対象が数万点〜数百万点になることが普通です。
行列式で表現可能なものは1つの行列式に整理しGPUで並列化する、は常に意識しておきたいところです。
前節では本題から外れましたが、回転・拡大変換を表す同次変換行列を紹介します。回転・拡大そのものには不要な1次元を追加して3×3にすると、次のように表されます。
- 拡大(ズーム)の同次変換行列:
\( Z_{HG} = \begin{bmatrix} a & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \)
- 回転の同次変換行列:
\( R_{HG} = \begin{bmatrix} cos\theta & -sin\theta & 0 \\ sin\theta & cos\theta & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \)
計算で確認しましょう。2次元座標平面上の同次座標\(P = (x, y, 1)^T\)をそれぞれ\( Z_{HG}, R_{HG} \)で変換すると、
\( Z_{HG}P = \begin{bmatrix} a & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix} = \begin{bmatrix} ax \\ by \\ 1 \\ \end{bmatrix} \)
\( R_{HG}P = \begin{bmatrix} cos\theta & -sin\theta & 0 \\ sin\theta & cos\theta & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} x \\ y \\ 1 \\ \end{bmatrix} = \begin{bmatrix} xcos\theta – ysin\theta \\ xsin\theta + ycos\theta \\ 1 \\ \end{bmatrix} \)
となりますから、3列目を無視して、1, 2列目を変換後の座標と見れば、正しく移動できていることがわかります。
2つ以上の変換を組み合わせて作れるより複雑な変換を合成変換といいます。
回転・拡大・並進は同次変換行列として全て同じ形状で表せますから、合成変換を表す行列は、単に行列積を作ることで計算可能です。
例えば、原点を中心\(\theta\)回転した後、\(x\)方向に\(p\), \(y\)方向に\(q\)並進する変換を表す行列は、
\( \boldsymbol A = Z_{HG}R_{HG} = \begin{bmatrix} a & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} cos\theta & -sin\theta & 0 \\ sin\theta & cos\theta & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} = \begin{bmatrix} cos\theta & -sin\theta & p \\ sin\theta & cos\theta & q \\ 0 & 0 & 1 \\ \end{bmatrix} \)
と覚えやすい形で表されます。ロボティクス分野では、回転の後、並進を行う合成変換を表すこの行列\(A\)が特によく使用されます。
同次変換は、行列積によって行うため、変換の順序が重要であり、順番を入れ替えてしまうと全く異なる結果になるため注意しましょう。
前節の行列\(\boldsymbol A\)の変換順序を逆にして、並進 -> 回転の順に変換する合成変換\(\boldsymbol B\)を計算してみます。
\( \boldsymbol B = R_{HG}Z_{HG} = \begin{bmatrix} cos\theta & -sin\theta & 0 \\ sin\theta & cos\theta & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} \begin{bmatrix} a & 0 & 0 \\ 0 & b & 0 \\ 0 & 0 & 1 \\ \end{bmatrix} = \begin{bmatrix} cos\theta & -sin\theta & pcos\theta – qsin\theta \\ sin\theta & cos\theta & pcos\theta + qsin\theta \\ 0 & 0 & 1 \\ \end{bmatrix} \)
となり、\(\boldsymbol A \neq \boldsymbol B\)ですね。
次節では、今までの内容をPythonで確認してみましょう。
また、本節のコード全文は、Jupyter Notebookの「3. Pythonによるハンズオンで確認する」をご覧ください。
Pythonコードの流れは以下のようになります。
- 変換行列
ZOOM_HG, ROTATION_HG, MOVE_HGを作る - 円を点群で表現し、1.の変換行列をかけて変換する
- 同様に、合成変換(例えば、回転 -> 並進)を表す変換行列を作り、2と同様に円を変換する
- 2で変換した円を図示し、変換前後の移動を確認する
- 3.で変換した円を図示する。また、回転 -> 並進と並進 -> 回転など、変換の順序によって結果が違うことを、図示により確認する
まず、3種類の変換行列を作成し変換した円を作ります。
3種類の変換のうち2種類を使用した合成変換は、6種類考えることができます。6種類の合成変換で変換した円を作成します。
行列式により、非常に簡潔にかけていますね。
最後に、変換前後の円を全てmatplotlibでプロットして確認します。
まずは、ズーム(拡大縮小)、回転、並進の変換前後の円を図示すると、以下のようになります。
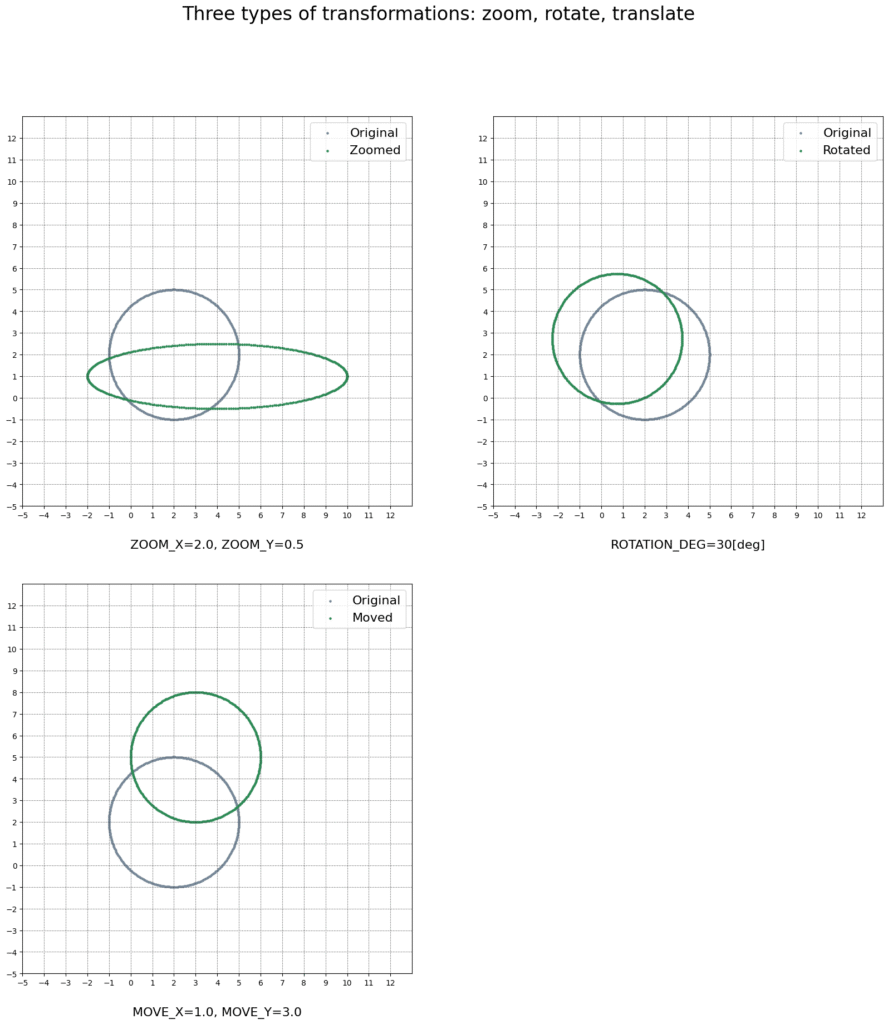
次に、合成変換6種類の変換前後の円をmatplotlibで図示します。
行列をかける順序(=変換の順序)によって、作られる合成変換も異なることを確認するために、例えばズーム -> 回転と、回転 -> ズームを同じ座標平面上に書いています。
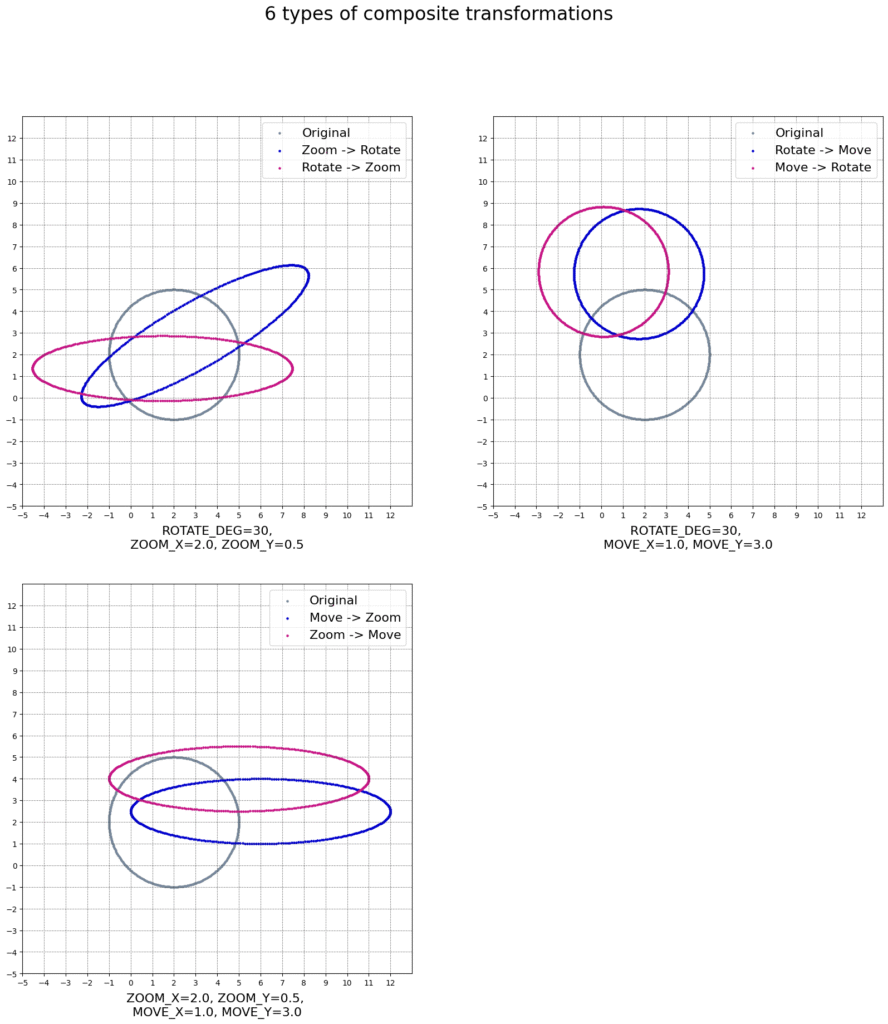
ズーム、回転、並進のうち、どの2つの変換をとっても交換可能ではないことが目で見て確認できますね。
多数の座標平面に共通のスタイリングを適用するために、オブジェクト指向のmatplotlibを採用し、自作クラスPltCoordPlanesを作成しています(参考リンク)。
本題から外れるので説明を省きましたが、詳細はJupyter Notebookを確認してください。
- 回転・拡大・並進は、同次座標に対する変換として、全て同じ形状の行列、同次変換行列で表せる
- 複数の変換が組み合わされた合成変換は、変換行列同士の行列積になる
- 変換同士は交換可能ではないため、順序が非常に重要
以上で、同次変換行列の基礎の説明を終わります。お疲れ様でした。



